Contents
PD Controller: Definition & Applications
The main application of PD controller is for controlling integrating processes (recall that in the field of linear control systems, integrating process refers to a process whose transfer function has a pole at the origin. Usually an integrating process also has a stable pole or a pair of complex conjugate stable poles in addition to the pole at the origin).
A DC motor with voltage as input and angular position as output is an example of integrating process. According to the internal model principle, a feedback control system with an integrating process in the forward path tracks the step setpoint without steady state error. So, the PID integral gain can be considered equal to zero, and a P only controller (also known as proportional controller or P controller) or a PD controller (also known as proportional derivative controller) should be used in dealing with integrating processes.
In either case increasing the proportional gain of the controller can speed up the feedback control system response. However, by closing the feedback loop with a P only controller, any attempt for speeding up the closed loop system by increasing the proportional gain usually leads to oscillatory response around setpoint, which is not desired in practice.
But, by closing the feedback loop with a PD controller it is possible to use much smaller values for proportional gain and avoid such an oscillatory response, and still speed up the closed loop response thanks to the derivative term of this controller. Note that the derivative term of PD controller has no effect on the response at steady state (corresponding to tracking of step setpoint or rejection of step disturbance). Note also that feedback control of an integrating process with a PI controller may not be possible because of closed-loop instability.
Most of the PID tuning methods like Ziegler-Nichols and CHR method do not have any option for designing PD controller. Rules for tuning the parameters of PD controller appear in a very few methods like the Cohen-Coon method (see here for more information).
PD Controller Design Example
Probably the best method for designing a PD controller is using the pidtune function of Matlab (see here for more information). Consider a plant with transfer function \(G(s)=\frac{1}{s(s+1)}\). Clearly, \(G(s)\) is an integrating process since it has a pole at the origin. Note that in this example we have considered an integrating process because otherwise it is practically useless to design a PD controller (why? because the tracking error caused by step command is not equal to zero at steady state, and no one likes this!).
In order to design a PD controller, build the following feedback control system in Simulink, where the unit step command enters at \(t=0\) and the unit step disturbance enters at \(t=10\) to the system. I let the Simulink designs the PD controller and then changed the setting to make the closed-loop system response faster. The transfer function of the resulting PD controller is obtained as \(C(s)=6+4.29\frac{s}{1+s/8.58}\).
Note that here we have also considered the bandwidth of the lowpass filter, which is embedded in series with the derivative term of PD controller, as a tuning parameter (the transfer function of this lowpass filter is \(\frac{1}{1+s/8.58}\). Hence, the PD controller actually has three tuning parameters: proportional gain, derivative gain, and bandwidth of the lowpass filter.
Figure 1 shows the results of a simulation where a unit step command and a unit step disturbance enter to the feedback control system at \(t=0\) and \(t=5\), respectively. Setpoint tracking seems pretty good, but the controller cannot remove the steady state error caused by step disturbance. The important lesson we learn is that even though PD controller can lead to zero steady state error in response to step command when the plant has a pole at the origin, it is unable of removing the steady state error caused by step disturbance.
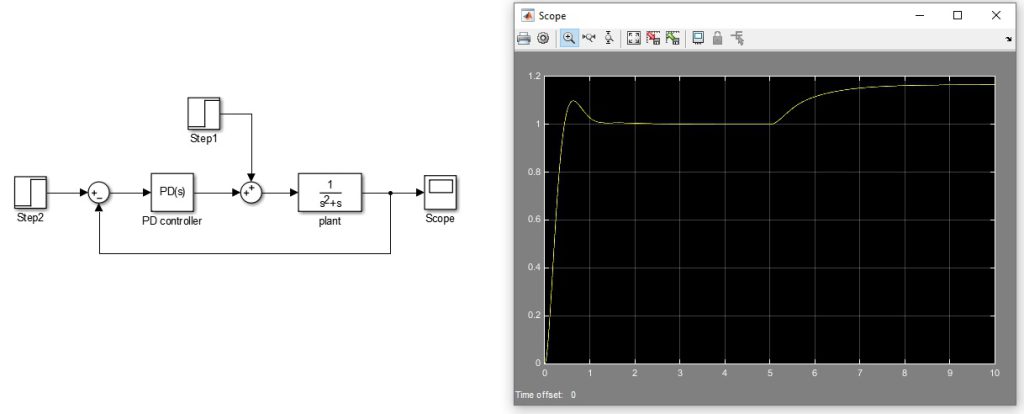
Fig. 1: Response of the closed-loop control system to step command and step disturbance
It concludes that in practice where step-like disturbances always exist, PD controller is not a good choice since does not lead to a satisfactory response even in dealing with integrating processes.
Are you interested in training films for control theory? Try this
Written by Farshad Merrikh Bayat, updated on September 7,2022
