Contents
Proportional Controller: Definition and Applications
Consider the feedback control system shown in Figure 1 where C(s) and G(s) stand for the controller and process transfer function, respectively, r(t) is the desired value (also known as command, reference or setpoint – SP) for the process output, and d(t) is the disturbance entered to the input of plant.
When C(s)=K, where K is a constant, we call it the proportional controller. Hence, proportional controller is a special case of C(s) which is in the form of a simple gain and does not have any dynamics. The reason for calling this kind of controller as proportional controller is that assuming d(t)=0 the control, which is denoted as u(t) in Fig. 1, is proportional to the tracking error e(t), that is u(t)=Ke(t).
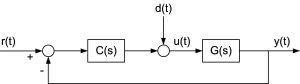
Fig. 1: feedback control system
Proportional controller can also be considered as a special case of proportional integral derivative (PID) controller where both the integral gain and derivative gain are considered equal to zero. The main drawback of proportional controller compared to the PID or PI controller is that it cannot eliminate the steady state error of the feedback control system to the step setpoint or disturbance.
The exception is controlling integrating processes where the transfer function of process has a pole at the origin and because of that pole, the feedback control system can track step setpoint without error at steady state. Note that even in dealing with an integrating process, the proportional controller is unable of removing the error to step disturbance at steady state (why?!) and a PI controller is required for this purpose.
Historically, proportional controller is invented and used much before than any other controller. Proportional controller was very popular in the very early practical control systems when the theory of control was not developed well and implementation of integrator was not possible.
The best way for designing a proportional controller for the given plant is the root locus method. For this purpose, assume that the plant model in the form of a transfer function is given. Determine the desired location (or region) for poles of the feedback control system in complex plane and choose the gain of proportional controller such that the poles of feedback control system lie inside the desired region.
Note that even in dealing with simple problems like water level control or speed control of DC motor it may not be possible to find the gain of proportional controller such that the above requirement is satisfied, and a more advanced controller like a PI may be required for this purpose.
The other problem with this kind of controller (and actually any other controller which is exerted in the feedback control system) is that it cannot change the location of zeros. In fact, open loop and closed loop control system have zeros exactly at the same locations. Hence, even if by calculating the gain of proportional controller we can put the poles of the feedback control system in the desired locations in complex plane, the response of feedback control system may not be as expected because of the effect of the zeros of plant transfer function.
The last point is that since the proportional controller only has one degrees of freedom, in a real world application one can adjust the proportional gain to the suitable value by a simple trial and error.
Proportional Controller in C
Implementation of proportional controller in C, or any other language, is very simple. Assume that \(e[k]\) is the tracking error at the \(k\)-th sampling period, i.e. \(e[k]=r[k]-y[k]\) where \(r[k]\) and \(y[k]\) are the reference and process output, respectively. Note that almost all of the micro-controllers are equipped with internal A/D converters. Hence, \(r[k]\) and \(y[k]\) are available as internal variables when you write the C code.
Assuming that the gain of proportional controller is equal to \(K\), the control \(u[k]\) is calculated as
\[u[k]=Ke[k]\]
In practice, the \(u[k]\) calculated from the above equation is converted to a PWM signal and then sent to one of the output pins of micro-controller.
Illustrative Design Example
In the following we show how this type of controller can be designed using the roots locus method. For this purpose consider the above feedback control system and assume that \(C(s)=K\) and \(G(s)=\frac{1}{s(s+1)}\). Note that the process transfer function has a pole at the origin which guarantees tracking step setpoint (but not rejecting the step disturbance which enters to the process input) without steady state error. Draw the root-locus plot of \(G(s)\) with Matlab to see the following figure.

By clicking on any point on the branches of plot, information of that point appears in a box as shown above. For example, it is observed that by considering \(K=0.457\) the closed-loop system has a pair of complex-conjugate poles with damping ratio \(0.74\) which leads to \(3.17\)% overshoot in the step-response of closed-loop system.
Are you interested in training films of the control theory? Have a look at this site.
Written by Farshad Merrikh Bayat | updated October 10, 2022
