Method 1: Ziegler Nichols (ZN) step response method

• Can be used for P controller, PI controller, and PID controller tuning (but not PD controller tuning)
• Only step response of the open loop system is required for P/PI/PID tuning
• response of the open loop system to step input can be oscillatory damped or in the form of a s shaped curve. The method can also be used for P controller/PI controller/PID controller design for an integrating process (DC motor and water level control are examples of integrating process).
• The purpose of controller design is to arrive at a closed loop system with a decay ratio of ¼ in response to a step disturbance which enters to the process input. Note that only disturbance rejection (but not command following) is under consideration in this method.
• The first big advantage of ZN step response method is that it needs very little information about the process. The second big advantage is that the P controller/PI controller/PID controller tuning formulas are summarized in user-friendly tables.
• The main disadvantage of this ZN PID/PI tuning method is that it usually leads to large overshoots in the response of closed loop system, especially when command following is under consideration. The reason is the damping ratio of the resulting feedback system is very small (approximately 0.2) since the proportional gain is 2-3 times larger than its appropriate value. The other drawback is that there is no table for PD controller design.
• Caution: This PID/PI tuning method does not lead to acceptable results for today’s applications. Never use it for current applications! There are much better methods as listed below.
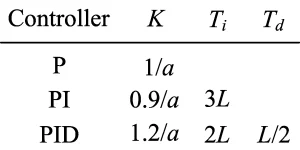
• Controller design algorithm: Draw the tangent line with maximum slope on the response of plant to the unit step input and determine parameters a and L (process delay) as shown in Figures 1 and 2 (which is a s shaped curve). Then calculate the P/PI/PID parameters from Table 1. The controller transfer function is where  and  are the PID integral and derivative time, respectively.

Fig. 1: response of an integrating process to step input

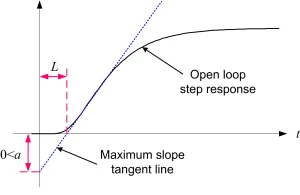
Fig. 2: s shaped step response

Table 1: P/PI/PID controller tuning using the Ziegler Nichols step response method

• Controller design example: Assume that the open loop process model is . Response of the open loop system to step input together with the maximum slope tangent line are shown in Figure 3. From this figure the values of a and L are obtained equal to 0.218 and 0.860, respectively, and the parameters of controller are calculated as , and . Response of the closed loop system to the unit step command and unit step disturbance (which enters at t=50s to the process input) with this controller in the feedback loop is shown in Fig. 4.

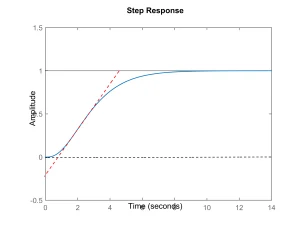
Fig. 3: response of the open loop control system to step input and the tangent line with maximum slope

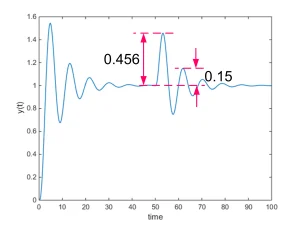
Fig. 4: response of the closed loop system to unit step