Method 2: Ziegler Nichols (ZN) frequency response method
Method 1: Ziegler Nichols (ZN) step response method
July 27, 2022Method 3: AMIGO PI controller tuning method
July 27, 2022- Can be used for P controller, PI controller, and PID controller tuning (but not PD controller tuning)
- Information of only one point on the Nyquist plot of the open loop system is required. This information can be obtained in two ways: relay feedback or proportional feedback. In both of these methods we put the series connection of process and a proportional controller or relay in a feedback loop and wait until stable oscillation appears at the output of process. The relay feedback method is more favorite since oscillation begins automatically. For this reason, this method for Proportional Integral Derivative controller design is referred to as PID/PI auto tuning (or, autotuning).
- The purpose of controller design is to arrive at a closed loop system with a decay ratio of ¼ in response to a step disturbance which enters to the input of plant. Note that only disturbance rejection (but not command following) is under consideration.
- The advantages and disadvantages of this PID/PI controller design method are the same as ZN step response method. The additional drawback of this method is that in order to find the information of the certain point on the Nyquist plot of process, the feedback system must oscillate which may be harmful in real world applications. Note that ZN frequency response method usually leads to smaller overshoots in the step response of the closed loop compared to the previous ZN method.
- Caution: This PID tuning method is obsolete since it does not lead to acceptable results for today’s applications. Don’t use it! There are much better methods as listed below.
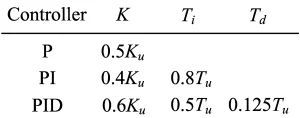
- Controller design algorithm: put the process in a unity feedback loop in series with a relay as shown in Fig. 5 where , and is the standard signum function. Hopefully oscillation begins automatically! At steady state, the process output and input are in the form of a (pseudo) sinusoidal wave and rectangular wave, respectively. Denote the ratio of the amplitude of input to the amplitude of output at steady state as , and the period of oscillation at steady state as . Then the parameters of proportional controller, PI controller, and PID controller can be calculated from Table 2 where the controller transfer function is considered as .

Fig. 5: relay feedback method
- Note that the ZN frequency response method actually moves the ultimate point on the Nyquist plot of plant (i.e. the point on the Nyquist plot which intersects the negative real axis) to -0.6-0.28j
- Controller design example: Assume that the open loop plant model is . If we put this plant in the closed loop system of Figure 5 the system begins oscillation. The input and output of plant in this case will be as shown in Fig. 6. As it is seen, the phase difference between input and output of plant at steady state approximately equals to 180 degrees. The period of oscillation at steady state is s, and we have (note that the corresponding exact values obtained from the Bode plot as shown in Fig. 6 are and ). Now, using Table 2 for PID controller design yields , and . Response of the feedback system to the unit step command and unit step disturbance (which enters at t=50s to the process input) with this PID controller in the feedback loop is shown in Fig. 8.
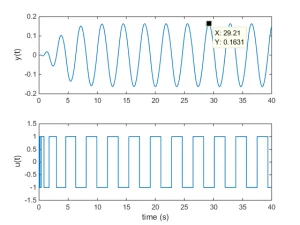
Fig. 6: stable oscillations using revvvlay feedback method
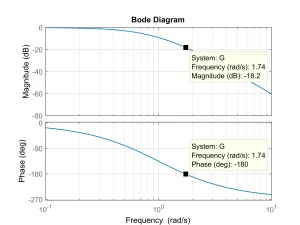
Fig. 7: Bode plot of the process model
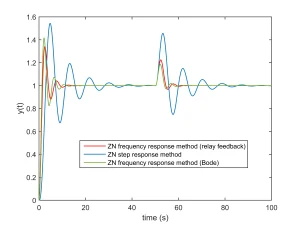
Fig. 8: response of the closed loop system to unit step vvvvvand unit step disturbance (which enters at the input of process at t=50 s)
Table 2: P/PI/PID controller tuning using the Ziegler Nichols frequency response method
Dr.Bayat
dr farshad
